Part 1: Decision Tree – Classification
How does a node split happen?
In classification trees, node splitting is done based on purity. The goal is to reduce impurity (like Gini or Entropy) as much as possible at each split.
Gini Impurity Formula:
Gini=1−∑i=1Cpi2Gini = 1 – \sum_{i=1}^{C} p_i^2Gini=1−i=1∑Cpi2
Where pip_ipi is the proportion of class iii in the node.
Sample Data (Classification)
| ID | Feature (X) | Class (Y) |
|---|---|---|
| 1 | 2 | A |
| 2 | 3 | A |
| 3 | 10 | B |
| 4 | 19 | B |
| 5 | 20 | B |
We will try to split based on X.
Try a Split: X <= 5
- Left node: X ≤ 5 → IDs 1, 2 → [A, A]
- Right node: X > 5 → IDs 3, 4, 5 → [B, B, B]
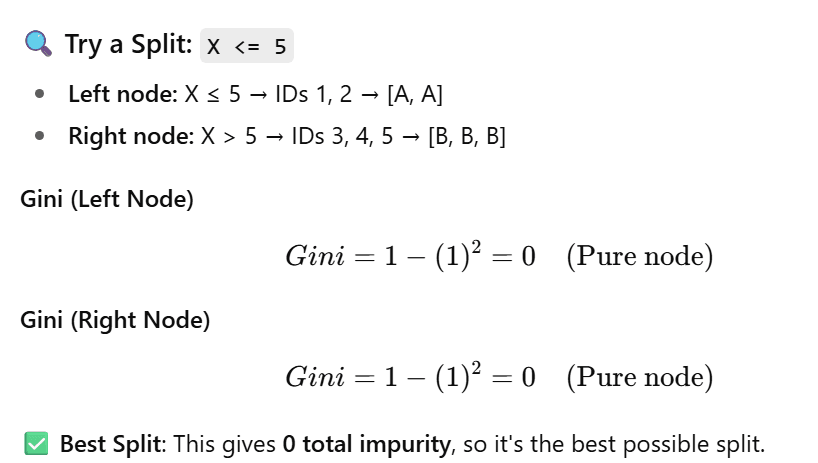
Best Split: This gives 0 total impurity, so it’s the best possible split.
Try another Split: X <= 15
- Left node: X ≤ 15 → IDs 1, 2, 3 → [A, A, B]
- Right node: X > 15 → IDs 4, 5 → [B, B]
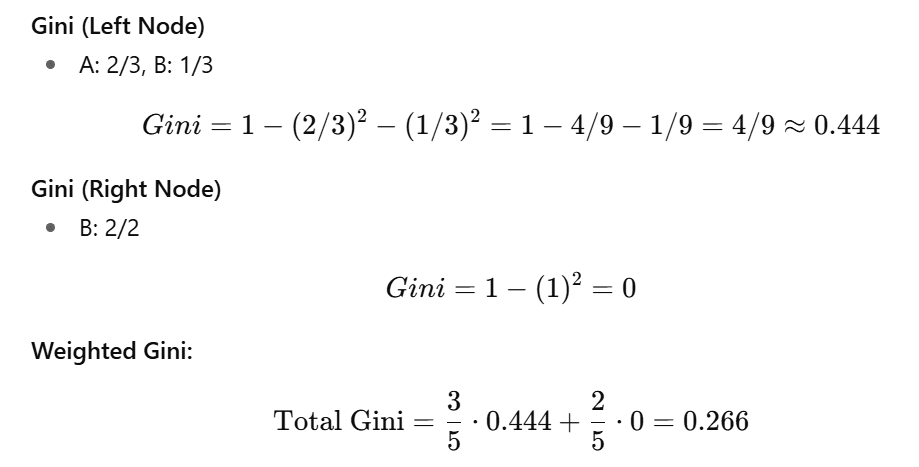
Higher than 0 → worse than first split.
Part 2: Decision Tree – Regression
How does a node split happen?
In regression trees, splitting is done to minimize variance (or MSE – Mean Squared Error) of the target variable.
Sample Data (Regression)
| ID | Feature (X) | Target (Y) |
|---|---|---|
| 1 | 2 | 5 |
| 2 | 3 | 6 |
| 3 | 10 | 13 |
| 4 | 19 | 25 |
| 5 | 20 | 26 |
Try a Split: X <= 5
- Left Node (X ≤ 5): IDs 1, 2 → [5, 6]
- Right Node (X > 5): IDs 3, 4, 5 → [13, 25, 26]
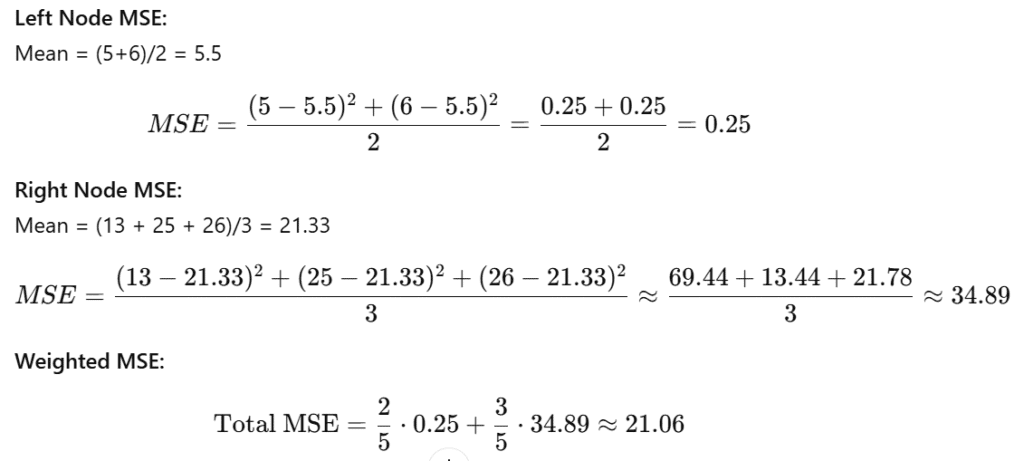
Try a Better Split: X <= 10
- Left Node: IDs 1, 2, 3 → [5, 6, 13]
- Right Node: IDs 4, 5 → [25, 26]
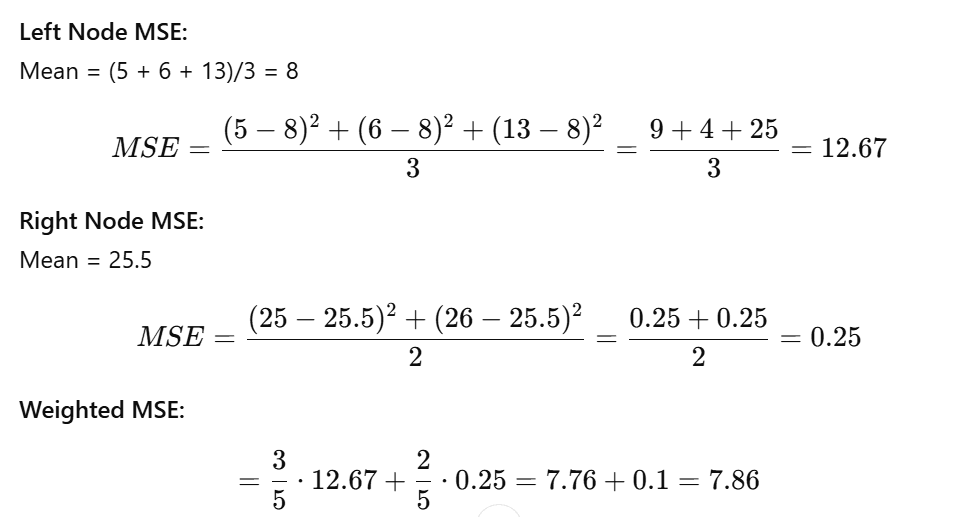
Much lower than 21.06 – better split.
Summary:
| Tree Type | Split Criteria | Objective |
|---|---|---|
| Classification | Gini Impurity (or Entropy) | Maximize class separation (purity) |
| Regression | MSE (or MAE, Variance) | Minimize variance (error) |